ディメンションWが負のXであるのはなぜですか？

単位ベクトル表記|ベクトルとスペース|線形代数|カーンアカデミー

彼らが次元Wを説明しているとき、それはX軸の負の側として表されます。ディメンションWが負のXであるのはなぜですか？それは本当にそれ自身の次元ではありませんか？

@NendoTakaが述べたように、2Dサーフェスに4Dオブジェクトを描画するのはかなり難しいです。

次元性の仕組みは次のとおりです。

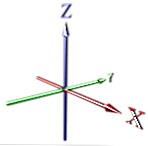
単一の次元では、点が無限に送信され、線が作成されます（Xを参照）

2Dでは、それに垂直な寸法を追加します（X、Yを参照）。

次に、再び垂直に移動し、上に拡張して3番目の次元を取得します（X、Y、Zを参照）。

3d> 2dであるため、紙を折りたたむか、その上にシートを追加しない限り、紙でそれをうまく表現することはできません。これらはすべて、画面で表示するには実際には実用的ではありません。したがって、代わりに遠近法を使用します。つまり、目が3Dをどのように認識するかです。通常、ここでの角度は約30度です。

私たちの目はこの伝統的な3Dの意味では見えないので、それはかなり問題ないように見えます。しかし、4次元を表現したい場合、それと比較するものはありません。私たちは再び垂直に行く必要があります、そしてこれは私たちが多くの参照を持っていないので私たちの目が理解するのは難しいです。

4次元の描写例を次に示します。

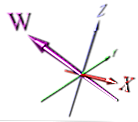
これは寸法を表示するためのより正しい方法ですが、それでも遠近法に依存しています。また、それが一見したところ新しい寸法であることがすぐにはわかりません。

アニメーターはおそらく、アニメートしやすい簡単なことをすることを選んだでしょう。ただし、上の画像を回転させると、XとWの寸法が重なる可能性があります。これは、矢印ポインタのない画像ではわかりません。

そうそう、それらは間違っています-しかし、1枚の紙に4次元を表す簡単な方法もありません

画像ソースを調整し、よく読む

1公平を期すために、正八胞体や3球などの4次元オブジェクトを、ショーで使用されているものよりもはるかに優れた3次元に（そして通常の方法では2次元に）投影する多くの標準的な方法があります。そのうち、ショーで使用されているものよりもクールに見えるという追加のボーナスがあります。
@senshin確かにそうですが、アニメーターも驚かされるのではなく、何かを説明したかったと思います
1位置以外のものを使用して、色など、軸に沿った距離を示すことができます。